7.6 Fundamentals of Heat Transfer

Frances Zhu

7. Thermal Control

7.6 Fundamentals of Heat Transfer

Heat Transfer Mechanisms

Conduction

Conduction is the direct transfer of heat that occurs between materials that 1) have physical contact and 2) have a relative temperature difference. “Conduction takes place in all phases: solid, liquid, and gas. The rate at which energy is conducted as the heat between two bodies depends on the temperature difference (and hence temperature gradient) between the two bodies and the properties of the conductive interface through which the heat is transferred” [Wikipedia].

Conduction is the primary heat transfer mechanism internal to the spacecraft. Heat flows from hot (high temperature) to cold (low temperature) until an equilibrium can be achieved. The basic law of one-dimensional heat conduction was formulated by Fourier in 1822. The amount of heat transfer $Q$ is proportional to the thermal conductivity $K$ , area $A$ , and thermal gradient $\tfrac{dT}{dx}$ .

$Q = - K A \tfrac{dT}{dx}$ .

Thermal conductivity can be defined in terms of the heat flow across a temperature difference. Image by Maxwell Molecule.

Thermal conductivity is a material property with units $\tfrac{W}{m \degree K}$ . Thermal conductivity is likened to electrical resistance in the way that both properties represent the ease at which energy transfers through a material. Common materials in spacecraft structures and their thermal conductivity are [Wikipedia]:

Material	Thermal Conductivity $\tfrac{W}{m \degree K}$	Spacecraft Use
Aluminum	237[6]	Structure
Copper (pure)	401[4][12][13]	Electrical interfaces and grounding planes
Silica aerogel	0.02[4]	Insulation
Water	0.5918[15]	Thermal regulation or propellant
Polycarbonate	0.2	Printed circuit board material

If we were to inspect a system more closely as to how heat “flows” in a solid, we need a general differential equation that describes how heat propagates spatially through time:

$\nabla^2 K T + \rho c \tfrac{\partial T(r,t)}{\partial t} = q(r,t)$

Where

q(r,t)=internally generated heat

ρ=density (kg/m3)

c=specific heat (J/kg°K)

This equation is used in models of heat diffusion, constituting the backbone of finite element analysis of temperature distribution across a body over time.

Convection

Convection is the transfer of heat through the movement of fluids. Convection is usually the dominant form of heat transfer in liquids and gases. Fluids utilize gravity for circulation. We don’t have much gravity or fluids in space so we will gloss over the physics.

Simulation of thermal convection. Red hues designate hot areas, while regions with blue hues are cold. A hot, less-dense lower boundary layer sends plumes of hot material upwards, and likewise, cold material from the top moves downwards. This illustration is taken from a model of convection in the Earth’s mantle. Image by Harroschmeling.

Radiation

“Thermal radiation is the emission of electromagnetic waves from all matter that has a temperature greater than absolute zero. Thermal radiation reflects the conversion of thermal energy into electromagnetic energy. Thermal energy is the kinetic energy of random movements of atoms and molecules in matter. All matter with a nonzero temperature is composed of particles with kinetic energy” [Wikipedia]. “Thermal radiation can be emitted from objects at any wavelength, and at very high temperatures such radiation is associated with spectra far above the infrared, extending into visible, ultraviolet, and even X-ray regions (e.g. the solar corona). Thus, the popular association of infrared radiation with thermal radiation is only a coincidence based on typical (comparatively low) temperatures often found near the surface of planet Earth” [Wikipedia].

In short, thermal radiation works through electromagnetic fields and does not need a medium for transport, so radiation works in a vacuum. Radiation is the only mechanism for the spacecraft to thermally interact with the space environment, which we use to dump or remove heat external from a spacecraft in orbit.

Materials with higher emissivity appear to be hotter. In this thermal image, the ceramic cylinder appears to be colder than its cubic container (made of silicon carbide), while in fact, they have the same temperature. Image by Bancquo.

Radiation is the primary heat transfer mechanism external to the spacecraft. Heat flows from hot (high temperature) to cold (low temperature) until an equilibrium can be achieved, just like conduction. The rate of heat transfer by emitted radiation is determined by the Stefan-Boltzmann law of radiation. The amount of heat transfer $Q$ is proportional to the emissivity $\epsilon$ , surface area $A$ , and absolute temperature in Kelvin $T$ . $\sigma$ is the Stefan-Boltzmann constant that has a value of $\tfrac{J}{s m^2 K^4}$

$Q = \sigma \epsilon A T^4$

The full form of the Stefan-Boltzmann equation is

$Q = \sigma \epsilon A (T^4 - T_{env}^4)$

where $T_{env}$ =environmental temperature (=3°K for space)

Two bodies in a thermal equilibrium within a cavity isolated from the environment. The arrows depict the radiant powers. The letters e and a stand for the emitted and absorbed radiation of the white body.CC BY-NC-SA 2.0. Image courtesy of SEOS.

Emissivity is a material property that indicates the radiation of heat from a body. Emissivity ranges from 0 (a ‘white’ body that reflects radiation) to 1 (a black body that absorbs all heat). Values between 0 and 1 signify a ‘grey’ body that partially reflects and absorbs at some ratio; emissivity is a dimensionless value. More formally, “emissivity is the ratio of the thermal radiation from a surface to the radiation from an ideal black surface at the same temperature as given by the Stefan–Boltzmann law” [Wikipedia]. Here are some common materials used in space and their emissivity values [EngineeringToolbox]:

Material	Emissivity	Spacecraft Use
Aluminum (Highly Polished)	0.039 – 0.057	Structure
Aluminum (Anodized)	0.77	Structure
Amorphous Silicon	0.45 – 0.8	Common solar cell material
Copper (plated, polished)	0.03 – 0.06	Electrical interfaces and grounding planes
Silica aerogel	0.79	Insulation
Water	0.95 – 0.96	Thermal regulation or propellant
Polycarbonate	0.90 – 0.97	Printed circuit board material

Absorptivity of the surface of a material is its effectiveness in absorbing radiant energy. For a given wavelength $\lambda$ , absorptivity $\alpha$ is equal to emissivity $\epsilon$ :

$\epsilon(\lambda) = \alpha(\lambda)$

However, there are some materials that absorb in a different wavelength than it emits, the emissivity and absorptivity are different:

$\epsilon(\lambda_{infrared}) \neq \alpha(\lambda_{visible})$

Various materials with differing emissivity and absorptivity are given below:

Material	$\alpha(\lambda_{visible})$	$\epsilon(\lambda_{infrared})$	Ratio
Aluminum	0.09	0.03	3.00
White paint	0.2	0.92	0.22
Black paint	0.92	0.89	1.03
Silver Teflon	0.08	0.8	0.1
Aluminized Kapton	0.38	0.67	0.56

These materials can be leveraged to achieve general warming or cooling effects. A ratio greater than 1 promotes warming and a ratio less than 1 promotes cooling. Some common strategies:

Use Silver Teflon to minimize solar absorption but max emissions (e.g., for telescope mirrors)
Use black paint to maximize energy transfer, both absorption and emission (interior)
Use metals (e.g., Aluminum) to minimize both absorption and emission (instrument sun shield)
Combine these surfaces to get almost any 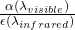$\tfrac{\alpha(\lambda_{visible})}{\epsilon(\lambda_{infrared})}$ you want

Radiation Interactions

Thermal Radiation to Space

Recall the Stefan-Boltzmann equation:

$Q_{out} = \epsilon(\lambda) \sigma T^4 A_{rad}$

Where $T$ is the temperature in Kelvin,

$A_{rad}$ is the surface area projected to space in $m^2$ ,

$\sigma = 5.67 \times 10^{-8} \tfrac{W}{m^2 K}$ is the Stefan-Boltzmann constant, and

$\epsilon(\lambda)$ is the emissivity of the surface, which depends on the wavelength $\lambda$ .

Note that the emissivity of different wavelengths is not equivalent: $\epsilon(thermal infrared) \neq \epsilon(visible)$ . But also that radiation is emitted at all wavelengths, so how do we distinguish what value of emissivity to use? We use Wien’s law to determine the wavelength that is most dominant.

Black-body radiation as a function of wavelength for various temperatures. Each temperature curve peaks at a different wavelength and Wien’s law describes the shift of that peak. CC BY-SA 3.0. Image by Curva Planck.

As a quick example, for a spacecraft with a surface emissivity of 0.8, a temperature of 330K, and a surface area projection of 1 $m^2$ , the heat radiating to space comes out at 538 Watts!

Solar Irradiance

Solar Radiation Spectrum.Creative Commons Attribution-Share Alike 3.0 Unported license. Image by Robert A. Rohde.

“The sun produces light with a distribution similar to what would be expected from a 5525 K (5250 °C) blackbody, which is approximately the sun’s surface temperature. These curves are based on NREL data for above the atmosphere and at sea level, which are standards adopted by the photovoltaic industry to ensure consistent test conditions and are similar to the light that could be expected in North America.” [Wikipedia].

For example, let’s take an example of white paint, where the emissivity is 0.8 but the absorptivity is 0.4. The incoming power from solar irradiance is given by:

$Q_{sun} = I_s \alpha_{visible} A_{sun}$

where $A_{sun}$ is the area perpendicular to the Sun vector and $I_s$ is the solar irradiance around Earth; see some similarities from the solar cell power equation? The incoming power for these parameters is 26.9 Watts.

A final note about the effect of solar radiation, outgassing deposit particles on surfaces that increase absorptivity but have almost no effect on emissivity.

Spectral absorptance/emittance of several materials and coatings. Image by Keyvan Niaki.

Albedo

Suggested Reading

Using real Earth Albedo and Earth IR Flux for Spacecraft Thermal Analysis

Example of daily albedo data (CERES). Image by Romain Peyrou-Lauga.

Reflected sunlight from planetary bodies comes in the form of albedo. Albedo is the fraction of solar irradiance reflected off a planetary body’s surface, most commonly calculated for the Earth. Albedo is a function of orbit and spacecraft attitude. Values for Earth oscillate between 0.2 to 0.6. $A_{Earth}$ is the area projected to Earth.

Illustration of effective albedo at any instant as perceived by an Earth-orbiting spacecraft.Peyrou-Lauga, Romain. “Using real Earth albedo and Earth IR flux for spacecraft thermal analysis.” 47th International Conference on Environmental Systems, 2017.Image by Romain Peyrou-Lauga.

To calculate the resultant heat coming from albedo:

$Q_{alb} = I_s \alpha_{visible} \cdot R \cdot A_{Earth}$

Where R is the albedo coefficient. Let’s do a sample calculation incorporating some example values where absorptivity $\alpha_{visible} =0.4$ , albedo $R=0.4$ , and $A_{Earth}=1 m^2$ . The resultant heat from albedo is 26.9 Watts.

Thermal Emission from Earth

The Earth’s radiation budget is incoming radiation to Earth must equal outgoing radiation. Absorbed solar radiation (short-wave) increases the Earth’s temperature, while emitted long-wave radiation (heat) lowers the temperature. Image by UMaine.edu.

The Earth not only reflects sunlight but emits heat as a radiative source. The earth absorbs heat from the sun and also generates its own heat from its dynamic, molten core. This heat is emitted nearby spacecraft with the following relationship:

$Q_{Earth} = \epsilon_{infrared} \cdot F \cdot \epsilon_{\alpha} \sigma T^4 A_{rad}$

Where F is a geometric factor called the view factor. View factor is a dimensionless factor between 0 and 1 that determines how much of a surface is visible to another surface and is a pure geometric property [Klobuchar]. Where F is a geometric factor called the view factor, $\epsilon_{infrared}$ is Earth’s emissivity, $\alpha_{infrared}$ is the absorptivity of the spacecraft during the infrared range

$F_{ij} = \tfrac{radiation leaving A_i and intercepted by A_j}{radiation leaving A_i}$

View factors are typically tabulated in calculators or spreadsheets. For interaction between a spacecraft and the Earth, the Nusselt Unit Sphere method calculates the view factor between a sphere and a flat surface.

For a sample calculation where the altitude is 500 km and the angle between the normals to the surfaces of the areas is 90 degrees, the view factor is 0.28. Earth’s emissivity $\epsilon_{Earth}$ is about 1, near perfect to a black body. The temperature $T$ is about 255 Kelvin. Area of radiation $A_{rad}$ is the spacecraft area perpendicular to Earth, which we’ll use 1 $m^2$ . The Earth’s emissivity is at 26.9 Watts.

Thermal Equilibrium

In thermal equilibrium, the heat power going in equals that going out. This result comes from the first law of thermodynamics: “the law of conservation of energy states that the total energy of an isolated system is constant; energy can be transformed from one form to another, but can be neither created nor destroyed” [Wikipedia]. The change in internal energy of a closed system $\Delta U$ is the difference in the heat going into the system $Q$ and the amount of thermodynamic work done by the system $W$ :

$Q - W = \tfrac{dU}{dt}$

For spacecraft, the heat going in $Q$ is the incident energy absorbed. The heat going out $W$ is radiated energy. The work done internally is internal power used (negative work in this sense – adds to total heat in the system).

Environment

Let’s look into a specific case for an Earth-centric spacecraft to demonstrate how to find equilibrium temperature.

The power going into the system is a result of direct solar irradiance $Q_{sun}$ , reflected sunlight (albedo) $Q_{alb}$ , thermal emission from Earth $Q_{Earth}$ , and internal heat sources $Q_{int}$ (like electronics and humans):

$Q_{in} = Q_{sun} + Q_{alb} + Q_{Earth} + Q_{int}$

The power going out of the system $Q_{out}$ is from a single sink: radiation to space, which depends on the surface temperature. The thermal balance equation is then:

$Q_{in} = Q_{out}(T)$

One equation and one unknown lead to a unique solution. This heat balance equation solves the equilibrium temperature for a single node, which is the spacecraft. This solution is the mean temperature of the entire spacecraft and does not inspect the temperature differences between different components within the spacecraft.

Effect of Distance on Equilibrium Temperature.Akin ENAE 483/788D – Principles of Space Systems Design Lecture Notes.

Surface Properties

Let’s gain some intuition as to how the equilibrium temperature varies with surface properties we can control, like satellite geometry and absorptivity/emissivity ratio. A shape absorbs energy only via illuminated faces but a shape radiates energy via all surface area. The basic assumption made is that black bodies are intrinsically isothermal (perfect and instantaneous conduction of heat internally to all faces). Although the balance includes the effects of the sun, albedo, Earth, and internal components, let’s simplify the balance to just include sunlight power and radiated power out:

$Q_{sun} = Q_{out}$

Where $Q_{sun} = I_s \alpha_{visible} A_{sun}$

And $Q_{out} = \epsilon(\lambda) \sigma T^4 A_{rad}$

The new balance with all variables include:

$I_s \alpha_{visible} A_{sun}} = \epsilon(\lambda) \sigma T^4 A_{rad}$

By isolating temperature on the left, we have:

$T^4 = \tfrac{I_s}{\sigma} \tfrac{\alpha_{visible}}{\epsilon(\lambda)} \tfrac{A_{sun}}{A_{rad}}$

There are three ratios that temperature scales with 1) constants that we cannot vary, 2) ratio of absorptivity and emissivity that we can change surface coatings, and 3) ratio of sunlit area to radiative area. The ratio of sunlit area to radiating area for various geometries is given below:

Geometry	Absorbing Area	Radiating Area	Area Ratio
Double-sided Wall	1	1	1/2
Sphere	$\pi r^2$	$4 \pi r^2$	1/4
Cylinder	$D \times H$	$\pi \times D \times H$	$\tfrac{1}{\pi}$
Cube	1	6	1/6

Something you’ll notice is that the more compact the spacecraft volume, the smaller the area ratio the lower the equilibrium temperature.

Effect of Shape on Black Body Temperature. Akin ENAE 483/788D – Principles of Space Systems Design Lecture Notes.

Internal Power Generation

60×60×10 mm straight-finned heat sink with a thermal profile and swirling animated forced convection flow trajectories from a tube axial fan, predicted using a CFD analysis package. CC BY-SA 3.0. Image by Isofilm .

Thus far, we have only talked about ideal heat transfer interactions. We need to include non-ideal effects that better reflect reality, such as power generation within the spacecraft. The spacecraft avionics will generate heat due to inefficiencies in using or transferring power, like when a current flows through a resistor in an electric circuit [Renesas]. The spacecraft may also have embedded heaters that intentionally or pointedly generate power. This generated power $Q_{int}$ is on the left-hand side of the equation as a part of the heat going into the system $Q_{in}$ .

When a semiconductor conducts current, there is a non-zero voltage drop across it. This results in losses that are converted almost entirely into heat. Consider the following simplified structure of a typical use case of an IGBT silicon chip and a diode silicon chip, mounted to a case that is mounted to a heat sink. For both the IGBT and diode, the heat power originates in the junction, where its value is the highest. The instantaneous value of power is equal to the resistance (I x V) of the IGBT or diode. The heat flows through the thermal impedance of the structure and dissipates in the ambient environment. The lower the thermal impedance, the lower the rise of the silicon temperature above ambient is. Image by My Electronic Days.

To calculate a ballpark number of power generated, measure the total power consumed by the electronics and multiply it by the useful efficiency. The lost power turns into heat through conduction, heating up the component:

$Q_{int} = (1 - \nu) P_{int}$

Where $\nu$ is the efficiency of the electronic part and

$P_{int}$ is the total power consumed by electronic components

For heaters, this same equation can be used by setting $\nu=0$ .

$Q_{int} = P_{int}$

For a lumped sum analysis, the system’s $Q_{int}$ is a summation of all the sources of heat within the spacecraft. For a more detailed finite element analysis, each heat source should also be associated with a location within the spacecraft.

Loading…

License

Icon for the Creative Commons Attribution 4.0 International License