6. Communications
6.6 Fundamentals in Signals
This section will walk through the fundamentals of signals, signal processing, and link budgets in the context of spacecraft. We’ll start from the way information is structured (low level) to the way information is transmitted (high level). These concepts are important to your principal investigator, who is relying on you to communicate quality payload data.
Analog/Digital Signals
Most information that satellites measure and transmit is continuous in nature. For example, the spectral radiance of an image (payload data) or the temperature of the battery (telemetry). Information can be transmitted through analog (continuous) or digital (discretized, bits) signals. Analog/Digital conversion transforms continuous quantities into bits. Both analog and digital communications are used in satellites, but most current satellite communications systems are digital because digital modulations are usually more robust to noise.

Quantization
Quantization is the conversion of a continuous physical quantity (e.g. voltage) into a digital number (bits). This involves quantization, which introduces quantization (rounding) error. The quantized value is given by the following equation:
![]()
Where ![]() is the range of the physical variable,
is the range of the physical variable, ![]() is the number of bits, and
is the number of bits, and ![]() is the physical variable.
is the physical variable.

An illustrative example: say we have temperature measurements that range from -100C to +100C. If we encode it with only 3 bits, that defines 8 levels. The quantization step is 200C/8 levels=25C (!).
- Any temperature between -100C and -75C is encoded as 000.
- Any temperature between -75C and -50C is encoded as 001
- …
- Any temperature between +75C and +100C is encoded as 111
Obviously, we need more bits because 25C is not an acceptable resolution. Typical resolutions are 8- 16 bits for most physical measurements – more is possible.
Sampling
Analog signals are continuous in time. To discretize them, we need to sample them at certain discrete time instants. The sampling frequency is the frequency with which we take samples of the continuous signal. For example, in Ariane 5, all functional sensors are sampled by the OBC at 4Hz (every 250ms).

The differences between sampling and quantization are [DifferenceBetween]:
- “In sampling, the time axis is discretized while, in quantization, y-axis or the amplitude is discretized.
- In the sampling process, a single amplitude value is selected from the time interval to represent it while, in quantization, the values representing the time intervals are rounded off, to create a finite set of possible amplitude values.
- Sampling is done prior to the quantization process.”
Aliasing
How often do we need to sample? It depends on how quickly the signal changes (its bandwidth). If we don’t sample fast enough, our sample may not be representative of reality.
For example, two sinusoidal signals with very different frequencies may look the same when sampled at a low frequency.

To counter aliasing, we follow the Nyquist theorem that states we must sample at least at ![]() = 2B (B=bandwidth).
= 2B (B=bandwidth).
Nyquist Theorem
The Nyquist-Shannon sampling theorem states:
“If a function ![]() contains no frequencies higher than
contains no frequencies higher than ![]() hertz, it is completely determined by giving its ordinates at a series of points spaced
hertz, it is completely determined by giving its ordinates at a series of points spaced ![]() seconds apart.”
seconds apart.”
Or in other words, we must sample at least at ![]() (in practice: 2.2B) where B is the band limit to guarantee a perfect reconstruction of the original continuous signal. Scientists and engineers use this theorem to decide how frequently to sample a phenomenon. If the scientific subject of interest occurs at
(in practice: 2.2B) where B is the band limit to guarantee a perfect reconstruction of the original continuous signal. Scientists and engineers use this theorem to decide how frequently to sample a phenomenon. If the scientific subject of interest occurs at ![]() Hertz, then the payload should sample at
Hertz, then the payload should sample at ![]() Hertz. If the attitude dynamic mode occurs at
Hertz. If the attitude dynamic mode occurs at ![]() Hertz, then the IMU should sample at
Hertz, then the IMU should sample at ![]() Hertz.
Hertz.
- If
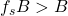 then we can low-pass-filter at B, and reconstruct the original signal perfectly
then we can low-pass-filter at B, and reconstruct the original signal perfectly - If
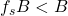 then there is overlap (aliasing) and we can’t reconstruct.
then there is overlap (aliasing) and we can’t reconstruct.

Coding

Source coding and channel coding are two different kinds of codes used in digital communication systems. They have orthogonal goals:
- The goal of source coding is data compression (decrease data rate).
- The goal of channel coding is error detection and correction (by increasing the data rate).

Source Coding
Source coding aims to code data more efficiently to represent information. This process reduces the “size” of data. For analog signals, source coding encodes analog source data into a binary format. For digital signals, source coding reduces the “size” of digital source data [Bouman].
Compression can be lossy or lossless. Lossless compression allows perfect reconstruction of the original signal. It is used when it is essential to maintain the integrity of the data. Lossless coding can only achieve moderate compression (e.g. 2:1 – 3:1) for natural images. Many scientists push for this in satellite missions. Examples include zip and png files.

In lossy compression, some information is lost and perfect reconstruction is not possible, but usually, a much higher reduction in bit rate is achieved. It is used when bit-rate reduction is very important and integrity is not critical. Lossy source coding can achieve much greater compression (e.g. 20:1 – 40:1) for natural images. Examples include jpg (images) and mp3 (audio) files.

Lossless compression methods usually exploit the structure of the information. A lossless compression algorithm is run-length encoding. Run-length coding is advantageous in that the data has sequences of the same data value occurring in many consecutive data elements. There are relatively long chains of 0’s or 1’s (infrequent changes). There are combinations of bits that are more likely than others. For example, in run-length encoding (RLE), runs of data are stored as a single value (count) rather than the original run, like so:
[1,0,0,0,0,0,0,0,0,0,0,1,1,…] → [1,10,2]
Note that this is only useful if there are many long runs of data (e.g. simple black and white images with mostly white)
Another type of lossless compression is Huffman coding where if some symbols are more likely than others, we can use fewer bits to encode the more likely combinations. That will result in reductions in bit rate without losing any information.

The final Huffman code is:
| Symbol | Code |
| a1 | 1 |
| a2 | 10 |
| a3 | 110 |
| a4 | 111 |
The standard way to represent a signal made of 4 symbols is by using 2 bits/symbol, but the entropy of the source is 1.74 bits/symbol. If this Huffman code is used to represent the signal, then the average length is lowered to 1.85 bits/symbol; it is still far from the theoretical limit because the probabilities of the symbols are different from the negative powers of two.
The Huffman coding algorithm follows:
- Assign 0 to the most likely symbol, the others start with 1.
- Assign 10 to the most likely symbol, the others start with 11.
- Continue…
Prefix codes: How do we tell when one symbol starts if they are variable in length? Prefix codes (like Huffman) don’t require any markers despite the variable length, because they are designed so that there is no possible confusion.
Channel Coding
Channel coding exists to ensure that the data received is the same as the data sent. “Wireless links suffer from interference and fading which causes errors, so to overcome this the transmitter adds additional information before the data is sent. Then at the receiver end, complex codes requiring sophisticated algorithms decode this information and recover the original data” [AccelerComm]. The act of detecting and correcting errors relies on a key idea: add redundancy bits strategically to avoid errors.
How do we detect an error? Imagine we add a parity bit at the end of every N bit so that the sum of all bits including the parity bit is always 0. Then we can detect one error:
- 01010101 → sum=0, OK no errors. (or there could be 2 errors!)
- 11101100 → sum=1, NOK. There’s an error (but can’t correct it)
How do we correct an error? Imagine that we simply transmit each bit 3 times. Then there are two possible symbols: 000 and 111. We say that the code has a distance of 3 because 3 bits need to change in order to change a valid symbol into another
- If we receive 100, 010, 001 → correct to 000
- If we receive 110, 101, 011 → correct to 111

If we detect an error, we can request a retransmission. This is sometimes called backward error correction. This is in opposition to forwarding an error correction (FEC) in which the error correction is embedded in the transmission.
Properties of FEC codes:
- Distance: Min number of bits needed to transform between two valid symbols
- Number of errors detected/corrected
- Rate: Number of data bits / Total number of bits
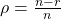
- Code gain: Gain in dB in link budget equation for equal BER (bit error rate)
Two major types of error-correcting codes:
- Block codes:
- Hamming codes
- Reed-Solomon
- Convolutional codes:
- Viterbi
“Hamming codes are a family of linear error-correcting codes. Hamming code is the shortened Hadamard code. Hamming codes can detect up to two-bit errors or correct one-bit errors without detection of uncorrected errors. By contrast, the simple parity code cannot correct errors and can detect only an odd number of bits in error. Hamming codes are perfect codes, that is, they achieve the highest possible rate for codes with their block length and minimum distance of three”.

All Hamming codes have distance 3, can detect 2 errors, and correct 1. Hamming code message lengths come in (![]() ): (total bits, data bits). For example:
): (total bits, data bits). For example:
- Hamming(3,1) is a message with triple repetition
- Hamming(7,4) is a message that adds 3 bits of redundancy to every 4 bits of data
- The rate of a block code is defined as the ratio between its message length and its block length. For this block code, the rate is 4/7.
Parity bits are added at positions 1, 2, 4, 8…The rest are data bits. Each parity bit covers a different subset of bits: parity bit 1 covers all bit positions that have the least significant bit set (1, 3, 5, …)

Intuitively, 1 error can be corrected thanks to the distance of 3 between valid symbols. Since each bit is assigned to a unique set of parity bits, we can identify which bit is wrong by identifying the bit for which all parity bits are the wrong d2. The position of the wrong bit is equal to the sum of the positions of all parity bits that are wrong: 1(p1) + 4(p3) = 5 (d2).

Another channel coding algorithm is called the Reed-Solomon error correction code. Instead of bits, the Reed-Solomon algorithm works on symbols (usually 8-bit blocks). This is better for burst errors because of multiple erroneous bits → 1 erroneous symbol. The code turns k data symbols into n > k symbols using polynomials.

- Encoding: Two steps
- Interpret message
![Rendered by QuickLaTeX.com x = [x_1, x_2, ... , x_k]](https://pressbooks-dev.oer.hawaii.edu/epet302/wp-content/ql-cache/quicklatex.com-21358cbd0645c04cda17e73db6f9d0b8_l3.png) as coefficients of a polynomial of degree
as coefficients of a polynomial of degree 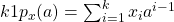
- Evaluate the polynomial at n different points:
![Rendered by QuickLaTeX.com C (x) = [p_x(a_1) , p_x(a_2) , ... , p_x (a_n) ]](https://pressbooks-dev.oer.hawaii.edu/epet302/wp-content/ql-cache/quicklatex.com-54aeb60dfbe7d1ce78467738de9a73f4_l3.png)
- Interpret message
- Decoding: Based on regression (find a polynomial that goes through the n points)
For example, Reed-Solomon (255,223) adds 32 redundant symbols for every 223 data symbols. It can detect 32 errors and correct 16. Read-Solomon is used exhaustively in space, especially in concatenation with convolutional codes (e.g. Voyager, Meteosat, Timed).


Modulations
Suggested Reading
Information between satellite and ground station is transmitted by changing some property (amplitude, frequency, or phase) of a high-frequency carrier signal c(t) in a way that encodes the information in the message m(t). This is called modulation. There is a modulation schema for analog and digital signals that we’ll review in this section.
Why do we need modulation? Why can’t we just transmit our train of pulses (bits)?
- These are very low-frequency signals
- Low-frequency signals would require extremely large antennas
- Low-frequency signals have huge atmospheric losses
Modulations are based upon modifying sinusoidal function. The three parameters in a sinusoid that can be changed are its amplitude, frequency, and phase.
Amplitude Modulation (AM)

“Amplitude modulation (AM) is a modulation technique used in electronic communication, most commonly for transmitting messages with a radio carrier wave. In amplitude modulation, the amplitude (signal strength) of the carrier wave is varied in proportion to that of the message signal” [Wikipedia]. This modular algorithm is easy to implement but has poor noise performance.

Let’s say the carrier signal at the licensed radio frequency has the form: ![]() . The analog signal is m(t) with bandwidth B, typically
. The analog signal is m(t) with bandwidth B, typically ![]() . Examples of analog signals are audio around 4kHz and video at 4Mhz. The amplitude modulated signal at the licensed radio frequency is
. Examples of analog signals are audio around 4kHz and video at 4Mhz. The amplitude modulated signal at the licensed radio frequency is ![]() .
.


Amplitude modulation requires:
- A local oscillator to generate the carrier high-frequency signal
- A mixer to mix (multiply) the two signals
- An amplifier

Demodulating the signal requires:
- A local oscillator to generate a proxy of the carrier signal
- A mixer to multiply
- A low-pass filter to keep only the low-frequency part of the received signal
- A diode to remove the DC part

Frequency Modulation (FM)

“Frequency modulation (FM) is the encoding of information in a carrier wave by varying the instantaneous frequency of the wave. The technology is used in telecommunications, radio broadcasting, signal processing, and computing. In radio transmission, an advantage of frequency modulation is that it has a larger signal-to-noise ratio and therefore rejects radio frequency interference better than an equal power amplitude modulation (AM) signal” [Wikipedia].

Let’s again assume a carrier signal of the form: ![]() . The analog signal that we are trying to convert is of form m(t) with bandwidth B, typically
. The analog signal that we are trying to convert is of form m(t) with bandwidth B, typically ![]() . The frequency modulated signal takes the form:
. The frequency modulated signal takes the form: ![]()
The spectrum of an FM signal is hard to compute analytically even for simple messages. FM modulation and demodulation are similar to AM in principle but require integrators and differentiators. Frequency modulation requires a frequency lock loop, which can be implemented with resistors, capacitors, and op-amps for example. “Direct FM modulation can be achieved by directly feeding the message into the input of a voltage-controlled oscillator. For indirect FM modulation, the message signal is integrated to generate a phase-modulated signal. This is used to modulate a crystal-controlled oscillator, and the result is passed through a frequency multiplier to produce an FM signal. In this modulation, narrowband FM is generated leading to wideband FM later and hence the modulation is known as indirect FM modulation. A common method for recovering the information signal is through a Foster-Seeley discriminator or ratio detector. A phase-locked loop can be used as an FM demodulator. Slope detection demodulates an FM signal by using a tuned circuit that has its resonant frequency slightly offset from the carrier. As the frequency rises and falls the tuned circuit provides a changing amplitude of response, converting FM to AM” [Wikipedia].

Phase Modulation
“Phase modulation (PM) is a modulation pattern for conditioning communication signals for transmission. It encodes a message signal as variations in the instantaneous phase of a carrier wave. Phase modulation is one of the two principal forms of angle modulation, together with frequency modulation. The phase of a carrier signal is modulated to follow the changing signal level (amplitude) of the message signal. The peak amplitude and the frequency of the carrier signal are maintained constant, but as the amplitude of the message signal changes, the phase of the carrier changes correspondingly. Phase modulation is widely used for transmitting radio waves and is an integral part of many digital transmission coding schemes that underlie a wide range of technologies like Wi-Fi, GSM and satellite television” [Wikipedia].

Let’s again assume a carrier signal of the form: ![]() . The analog signal that we are trying to convert is of form m(t) with bandwidth B, typically
. The analog signal that we are trying to convert is of form m(t) with bandwidth B, typically ![]() . The frequency modulated signal takes the form:
. The frequency modulated signal takes the form: ![]()

Phase modulation requires a phase lock loop control system. “There are several different types; the simplest is an electronic circuit consisting of a variable frequency oscillator and a phase detector in a feedback loop. The oscillator generates a periodic signal, and the phase detector compares the phase of that signal with the phase of the input periodic signal, adjusting the oscillator to keep the phases matched” [Wikipedia]. Most digital modulation techniques involve PM.
Digital Modulation
Instead of modulating an analog signal, digital modulation transforms a binary signal. The carrier signal is still an analog signal. In digital modulation, we use a finite number of analog signals (pulses) to represent pieces of a digital message i.e. we encode 00 as ![]() .
.
- For example, we can encode a 0 as
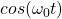 and a 1 as
and a 1 as 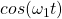
- This is Frequency Shift Keying (FSK). In FSK, different symbols (e.g. 0, 1) are transmitted at different frequencies
- In binary FSK, there are only 2 frequencies (0:
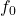 , 1:
, 1: 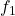 )
) - We can also have 4-FSK, 8-FSK, etc.
- 4-FSK: 00:
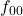 , 01:
, 01: 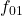 , 10:
, 10: 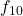 , 11:
, 11: 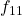
- In binary FSK, there are only 2 frequencies (0:
- This is Frequency Shift Keying (FSK). In FSK, different symbols (e.g. 0, 1) are transmitted at different frequencies

- Or we can encode a 0 as
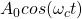 and a 1 as
and a 1 as 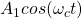
- This is Amplitude Shift Keying (ASK). In ASK, symbols correspond to different amplitudes.
- In binary ASK, we use 2 amplitudes, 0:
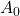 , 1:
, 1: 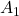 where typically
where typically 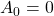
- We can also have 4-ASK, 8-ASK
- 4-FSK: 00:
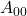 , 01:
, 01: 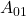 , 10:
, 10: 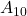 , 11:
, 11: 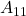
- 4-FSK: 00:

- Or we can encode a 0 as
 and a 1 as
and a 1 as 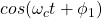
- This is Phase Shift Keying (PSK). In PSK, symbols correspond to different amplitudes.
- In binary PSK (BPSK), we use 2 phases, 0:
 , 1:
, 1: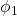 where typically
where typically 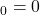 and
and 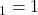
- We can also have 4-PSK (QPSK), 8- PSK…
- QPSK: 00:
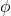 00 = 0,01:
00 = 0,01: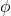 01 =
01 =  , 10:
, 10: 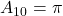 , 11:
, 11: 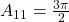
- QPSK: 00:

Quadrature Amplitude Modulation
“Quadrature amplitude modulation (QAM) conveys two analog message signals, or two digital bit streams, by changing (modulating) the amplitudes of two carrier waves, using the amplitude-shift keying (ASK) digital modulation scheme or amplitude modulation (AM) analog modulation scheme. The two carrier waves of the same frequency are out of phase with each other by 90°, a condition known as orthogonality or quadrature. The transmitted signal is created by adding the two carrier waves together” [Wikipedia]. QAM applies to both analog and digital information or message signals.

Let’s again assume a carrier signal of the form: ![]() and the 90 degree phase lag is of the form:
and the 90 degree phase lag is of the form: ![]() . “In a QAM signal, one carrier lags the other by 90°, and its amplitude modulation is customarily referred to as the in-phase component, denoted by I(t). The other modulating function is the quadrature component, Q(t). So the composite waveform is mathematically modeled as”:
. “In a QAM signal, one carrier lags the other by 90°, and its amplitude modulation is customarily referred to as the in-phase component, denoted by I(t). The other modulating function is the quadrature component, Q(t). So the composite waveform is mathematically modeled as”:
![]()
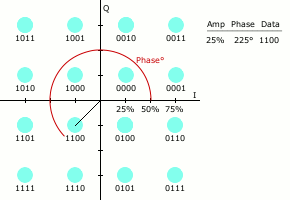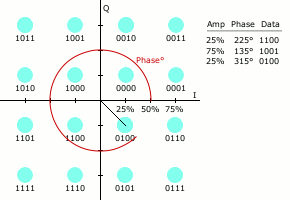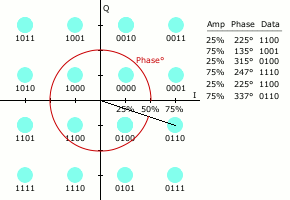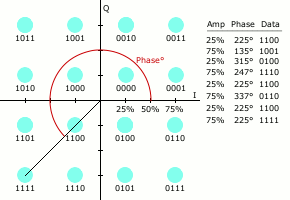
“As in many digital modulation schemes, the constellation diagram is useful for QAM. In QAM, the constellation points are usually arranged in a square grid with equal vertical and horizontal spacing, although other configurations are possible (e.g. Cross-QAM). Since in digital telecommunications the data is usually binary, the number of points in the grid is usually a power of 2 (2, 4, 8, …). Since QAM is usually square, some of these are rare—the most common forms are 16-QAM, 64-QAM, and 256-QAM. By moving to a higher-order constellation, it is possible to transmit more bits per symbol. However, if the mean energy of the constellation is to remain the same (by way of making a fair comparison), the points must be closer together and are thus more susceptible to noise and other corruption; this results in a higher bit error rate and so higher-order QAM can deliver more data less reliably than lower-order QAM, for constant mean constellation energy. Using higher-order QAM without increasing the bit error rate requires a higher signal-to-noise ratio (SNR) by increasing signal energy, reducing noise, or both” [Wikipedia].
Digital vs. Analog Modulation
In summary, analog and digital modulation modify an information signal with a carrier signal. The carrier signal is always a sinusoid at the licensed radiofrequency. The information signal can either be analog or digital, which defines the name of the modulation scheme.
The advantage of analog amplitude modulation conserves bandwidth and analog frequency modulation spreads information bandwidth over larger RF bandwidth. Digital pulse-code modulation (particularly phase-shift keying) uses RF power most efficiently.

“All modern spacecraft utilize pulse code modulation (PCM) to transfer binary data between the spacecraft and the mission operations. The data are phase-modulated onto an RF carrier (PCM/PM) or used to switch the phase of a subcarrier by plus or minus 90-degrees. The subcarrier is then phase modulated on the carrier for transmission via the space link. This modulation scheme is referred to as PCM/PSK/PM. Phase modulation is used because it has a constant envelope that enables non-linear amplifiers to be used. Non-linear amplifiers tend to be more efficient than the linear amplifiers that would be necessary if the envelope (amplitude) were used to carry information. Phase modulation is also immune to most interference that corrupts signal amplitude” [O’Dea & Pham].
Polarization

Polarization refers to the orientation of the electric field vector, ![]() . Waves can have different shapes: linear and circular. The shape is traced by the end of the vector at a fixed location, as observed along the direction of propagation.
. Waves can have different shapes: linear and circular. The shape is traced by the end of the vector at a fixed location, as observed along the direction of propagation.

Bit Error Rate (BER)
The Bit Error Rate is the probability that an error will be made in one bit when decoding a symbol. It is a measure of the quality of the communications, and one of the main requirements of a communications system. The other one is the data rate (i.e. the quantity of data). As an example, assume this transmitted bit sequence:
0 1 1 0 0 0 1 0 1 1
and the following received bit sequence:
0 0 1 0 1 0 1 0 0 1,
The number of bit errors (the underlined bits) is, in this case, 3. The BER is 3 incorrect bits divided by 10 transferred bits, resulting in a BER of 0.3 or 30%. Typically, BER is on the order of ![]() . Lower BERs can be accepted for non-critical applications.
. Lower BERs can be accepted for non-critical applications.
BER depends on two main parameters:
- The signal to noise ratio (typically expressed in terms of
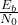 ), which is the ratio of Bit Energy to Noise Density.
), which is the ratio of Bit Energy to Noise Density. - The modulation that is chosen: for example, for the same BER, BPSK and QPSK require 3dB less of
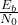 than 8PSK.
than 8PSK.
“In a communication system, the receiver side BER may be affected by transmission channel noise, interference, distortion, bit synchronization problems, attenuation, wireless multipath fading, etc. The BER may be improved by choosing a strong signal strength (unless this causes cross-talk and more bit errors), by choosing a slow and robust modulation scheme or line coding scheme, and by applying channel coding schemes such as redundant forward error correction codes. The transmission BER is the number of detected bits that are incorrect before error correction, divided by the total number of transferred bits (including redundant error codes). The information BER, approximately equal to the decoding error probability, is the number of decoded bits that remain incorrect after the error correction, divided by the total number of decoded bits (the useful information). Normally the transmission BER is larger than the information BER. The information BER is affected by the strength of the forward error correction code” [Wikipedia].

Let’s walk through computation of BER=f( ![]() ) for Binary Phase-Shift Keying (BPSK). We have a BPSK with a carrier signal where t is time and T is period, and the information signal is given by:
) for Binary Phase-Shift Keying (BPSK). We have a BPSK with a carrier signal where t is time and T is period, and the information signal is given by:
![]() and
and ![]()
Assume that the channel (i.e. the atmosphere and transceiver electronics) adds a Gaussian white noise n(t) of the mean of 0 and variance of
![]()
Then, the probability distribution of the received signal is a Gaussian centered around +A or −A depending on which symbol was transmitted.

Note that the two probability distributions overlap. If they didn’t, we could come up with a perfect decision rule that would always tell us what is the right symbol from the voltage in the receiver. This could be the case for noise with smaller variance or of a different shape, like a triangular noise with a bandwidth less than A.
The best imperfect rule that minimizes the probability of error is found with the Maximum A Posterior rule. Intuitively, in this simple case, we should just decide that a 1 was sent if the voltage received is positive, and 0 if it is negative. In general, this is a well-known classification problem (a.k.a. hypothesis testing) whose answer is known. Given this decision rule, the residual probability of error (BER) is:
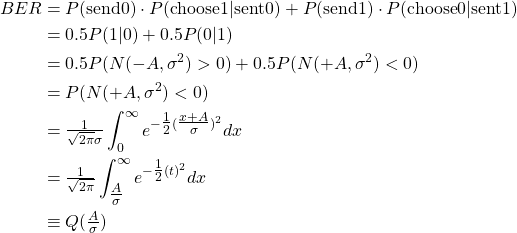
Typically, ![]() is expressed in terms of
is expressed in terms of ![]()
The BER can be computed for other modulations using a similar approach. For
example:

Adding coding schemes (Reed Solomon, Viterbi) to a modulation has the effect of pushing the BER=![]() curve towards the left (less power required for a given
curve towards the left (less power required for a given ![]() .
.
