Place Value
Other Rules
Let’s play the dots and boxes game, but change the rule.
The 1←3 Rule
Whenever there are three dots in single box, they “explode,” disappear, and become one dot in the box to the left.
Example: Fifteen dots in the 1←3 system
Here’s what happens with fifteen dots:
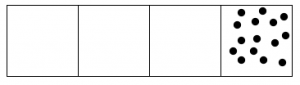

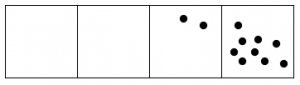




Solution: The 1←3 code for fifteen dots is: 120.
Problem 2
- Show that the 1←3 code for twenty dots is 202.
- What is the 1←3 code for thirteen dots?
- What is the 1←3 code for twenty-five dots?
- What number of dots has 1←3 code 1022?
- Is it possible for a collection of dots to have 1←3 code 2031? Explain your answer.
Problem 3
- Describe how the 1←4 rule would work.
- What is the 1←4 code for thirteen dots?
Problem 4
- What is the 1←5 code for the thirteen dots?
- What is the 1←5 code for five dots?
Problem 5
- What is the 1←9 code for thirteen dots?
- What is the 1←9 code for thirty dots?
Problem 6
- What is the 1←10 code for thirteen dots?
- What is the 1←10 code for thirty-seven dots?
- What is the 1←10 code for two hundred thirty-eight dots?
- What is the 1←10 code for five thousand eight hundred and thirty-three dots?
Think / Pair / Share
After you have worked on the problems on your own, compare your ideas with a partner. Can you describe what’s going on in Problem 6 and why?
