Introduction

Wind is the movement of air relative to the Earth’s surface. As with all moving things, it is caused by a force acting on it. Force is a pull or push that changes the resting state, motion, or direction of an object. Force can also cause objects to accelerate. Human skin can sense wind when an uncountable number of molecules collide with us as they flow along in the air, and sense the pressure changes in the air flow.

Main forces

There are five forces that influence the speed or direction of horizontal winds.

1. Pressure gradient force
2. Advection
3. Centrifugal force
4. Coriolis force
5. Turbulent drag

Remember from Chapter 1 that according to the Cartesian coordinates, x points east, y points north, and z points upwards. To define wind, we use wind components u, v, and w which correspond to the x, y, and z directions. These wind components are used in equations of motion used to predict wind to designate direction in a three-dimensional plane. We’ll go through each of the five forces one by one to discuss how they affect wind speed and/or direction.

Pressure Gradient Force

A pressure gradient (PG) is a change in pressure over a distance. Therefore, the units of the pressure gradient force are Pascals per meter (P m^-1). The pressure gradient can be calculated simply as the change in pressure divided by the distance over which that change occurs.  The size or strength of the pressure gradient determines the size or strength of the force that results from it. 

The pressure gradient force (PGF) is a force from high to low pressure over a distance. Without differences in pressure, there would be no wind because there would be nothing to accelerate airflow. In Chapter 9 we learned about isobars, or lines of constant pressure. When isobars are tightly packed, we know that there is a strong pressure gradient or large change in pressure over a relatively short distance. A strong pressure gradient results in a large pressure gradient force and, as we’ll see, higher wind speeds. Depending on the text you read, you’ll see a number of different forms of the pressure gradient force.  Two equivalent representations are given below.

The PGF as defined above is simply a change in pressure divided by the distance and air density. This gives the force per unit mass, hence PGF/m. Above we define PGF in the x-direction, but it can act in any horizontal plane. The units of the PGF will be in units of acceleration above because Force = Mass * Acceleration, but because we’re dividing the left-hand side by Mass the units will be m s^-2. The negative signs in the above equation is due to the fact that the PGF acts from high pressure to low pressure.

Another equivalent way to represent the PGF is as follows.

Because Mass = Volume * Density, we then see that Volume = Mass/Density. The second equation is identical to the first, except that Mass/Density is on the right hand side in the form of Volume instead of being split between left and right sides of the equals sign.  Also, the variable L is used for length or distance instead of Δx so that it isn’t for a specific direction. Similarly, the absolute value of the PGF is calculated, and the direction is determined, by the location of High and Low pressure systems. Typically in class we won’t calculate the PGF, only the PG. However, it’ll be widely used in force balance equations.

Advection

While advection is included in the list of forces, it is actually not a true force. Still, advection can result in a change of wind speed in some locations. Wind moving through a point carries specific momentum, which is defined as momentum per unit mass. Recall that momentum is mass times velocity. Specific momentum then is simply equal to the velocity or wind speed. Therefore, as wind moves by a point, the wind can move or advect variations in winds to the fixed location.

Centrifugal Force

The centrifugal force is an apparent force that includes the effects of inertia for winds moving along a curved path. The directionality of the centrifugal force points outward from the center of the curve. The centrifugal force is the opposite of the centripetal force. As we know, inertia is the physical tendency to remain unchanged. Therefore inertia causes an air parcel to “want” to move along a straight line. Turning the air parcel along a curved path requires a centripetal force that pulls inward to the center of rotation. As a result, a net imbalance of other forces occurs.

You have felt the centrifugal force many times in your life. The centrifugal force is easily felt as you travel in a moving vehicle around a corner. The force that you feel pulling you outwards is the centrifugal force.

Coriolis Force

The Coriolis force (CF) is another apparent force that occurs due to the rotation of Earth. The Coriolis force is a deflecting force. It acts only on objects already in motion. Therefore it cannot create wind, but it can change the wind direction by deflecting it. The Coriolis force acts perpendicular to the direction of motion, but whether the Coriolis force acts 90° to the right or left of the motion vector depends on the hemisphere on Earth. In the Northern Hemisphere, the Coriolis force acts 90° to the right of the motion vector while in the Southern Hemisphere, the force acts 90° to the left of the motion vector. The equation below gives the Coriolis force

where m is for the mass of the object in kg, u is the speed of the object in m s^-1, the symbol Φ denotes latitude in degrees, and the angular rotation rate, Ω, is found from the rotation rate of Earth. Earth turns 2*pi radians over 24 hrs, so 2*pi/24 hrs gives Ω = 7.27E-5 radians·s^–1.  Based on this, we can see that the Coriolis parameter will be 0 at the equator when sin(0)=0 and maximized at the poles when sin(90)=1.

We can also see that the Coriolis force is strongly dependent on the speed of the object. If we assume the “object” is actually wind, stronger winds will be more strongly deflected by the Coriolis force.

Turbulent Drag

Turbulent drag occurs when Earth’s surface or objects on it cause resistance to airflow and reduce the wind speed. Any object on Earth’s surface can cause drag, such as grass, trees, and buildings, which block and decelerate wind. The bottom layer of the troposphere around 0.3 to 3 km thick is called the atmospheric boundary layer (ABL). Turbulence in the ABL mixes the extremely slow movement of air near the surface with the faster movement of air in the ABL and slows the wind speed in the entire ABL.

Force Balances

The five forces from above affect aspects of horizontal wind speed and direction, and result in a number of common force balances found throughout Earth’s atmosphere.

Geostrophic Balance

Geostrophic balance is arguably the most important force balance in the atmosphere and holds nearly all the time, except for a few specific cases scenarios to be discussed later. When in geostrophic balance, wind in the atmosphere has a balance between the pressure gradient force and the Coriolis force. In geostrophic balance, PGF = CF. The resulting wind is called a geostrophic wind. Setting the equation for CF and PGF equal to each other and solving for u gives the following equation for U_geos.

Because geostrophic winds are dependent on the pressure gradient, geostrophic winds are faster when isobars are closely spaced.

A number of assumptions are implicit to geostrophic balance. Geostrophic balance applies only under the following conditions: large temporal (>12 hrs) and large spatial (> a few km) scales; above the ABL when no surface friction is acting on the air; winds are steadily moving in a straight direction (no acceleration, negligible vertical velocity); finally, because the Coriolis force is important for the balance, it cannot hold at the equator when the CF is 0. The typical bounds are often given as >2° latitude.

The path of the geostrophic wind is parallel to the isobars. In the Northern Hemisphere, the wind direction is parallel to the straight isobars with the low pressure to the left side of wind. In the Southern Hemisphere, the direction is parallel to the straight isobars with the low pressure to the wind’s right. The image below shows the force balance present in a geostrophic wind in the northern hemisphere.

To get into geostrophic balance, moving air will undergo geostrophic adjustment. First, air feels the pressure field (PGF) and begins moving from high to low pressure. Next, the Coriolis force (CF) deflects the object’s direction once it is in motion. Finally, the air finds itself in a balance between the PGF and the CF moving parallel to the isobars instead of across them.

Gradient Wind

This next force balance applies when air is not moving in a straight line. Gradient winds are winds flowing along curved isobars. Winds typically blow along isobars, even if they are curved, but a different name is needed because the force balance includes one more component. Compared to geostrophic winds, gradient winds feature a balance between the Coriolis force, the pressure gradient force, and the centrifugal force. The centrifugal force arises because the air is flowing on a curved path. The centrifugal force acts in the same direction as the coriolis force, opposite the pressure gradient force.

Atmospheric Boundary Layer

Balanced wind in the atmospheric boundary layer (ABL) occurs when there is a balance between the pressure gradient force, Coriolis force, and the frictional drag force. Both wind shear turbulence and convective turbulence cause drag, which results in the ABL wind being slower than geostrophic (subgeostrophic), and causes the wind to cross isobars toward the low pressure.

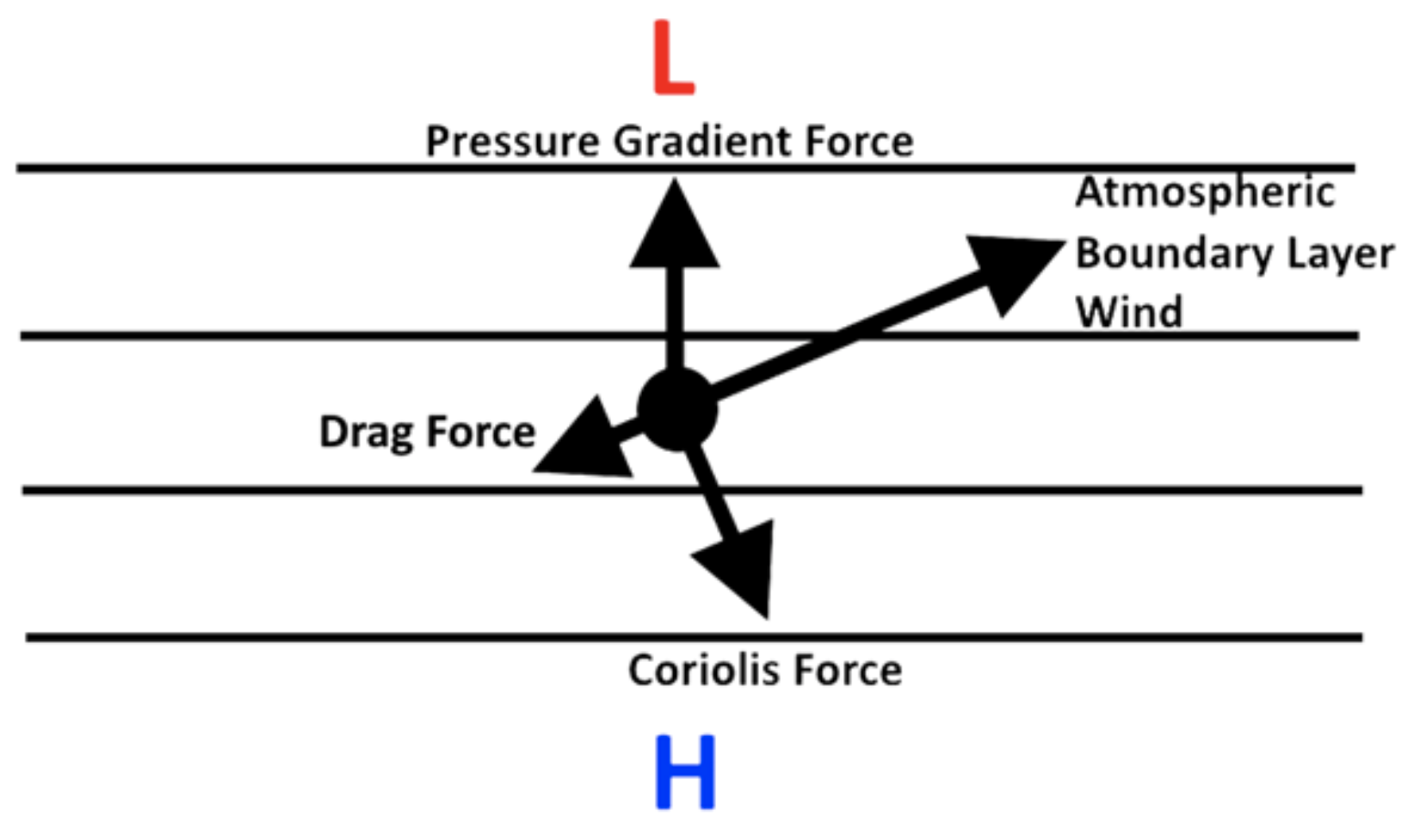
Again, the frictional drag force acts in the plane of motion and slows down the wind speed. The pressure gradient force doesn’t change, but because the wind speed is slower, the Coriolis force is weaker. When that happens the wind cannot balance the pressure gradient force, it is pulled more by the pressure gradient force, and turns toward the low pressure.

Cyclostrophic Wind

Cyclostrophic wind occurs at smaller cyclonic scales (at the mesoscale) such as tornadoes, waterspouts, and even the center of a tropical cyclone. Because the scale is small, the Coriolis force does not play a role. When a small cyclonic scale such as a tornado first forms, both tangential winds and centrifugal force increase much faster than the Coriolis force due to the very strong pressure gradient force. As a result, centrifugal force balances with the pressure gradient force, ignoring the negligible effects of Coriolis force. Because the scale is small and independent of the Coriolis force, the direction of cyclostrophic winds can be either clockwise or counterclockwise in both hemispheres. For anticyclones or highs, however, they do not typically have strong pressure gradients. Thus, winds around the high are too weak to be in cyclostrophic balance.

All of the wind balances discussed (geostrophic balance, gradient wind, ABL wind, and cyclostrophic wind) occur in Earth’s atmosphere under differing conditions. The following chapters will make these applications clearer and you can check back here for reference.