Chapter 2: Solar and Infrared Radiation
Alison Nugent
Learning Objectives
By the end of this chapter, you should be able to:
- Define black body radiation and Planck’s Law
- Apply Wien’s law to compute the maximum emission wavelength
- Use Stefan-Boltzmann’s law to compute radiative emittance
- Describe Earth’s surface radiation budget, including shortwave and longwave components
- Define and differentiate obliquity, eccentricity, and precession
- Describe the cause of seasons on Earth
- Describe the diurnal cycle of radiative fluxes
Introduction
Outside on a sunny day, you can feel the sun’s energy on your skin. You can feel it in the form of heat due to the transfer of energy between objects. Standing under the shade of a tree (which blocks the sun’s rays) makes a significant difference in temperature and your probability of getting a sunburn. The closest Earth gets to the Sun is approximately 93 million miles. How does the sun’s energy reach so far? The answer is in radiation. Radiation is the primary mechanism of energy transfer on Earth, including the transfer of energy from the Sun to the Earth over great distances through the vacuum of space.

Radiation
Radiation can be thought of in two ways: electromagnetic waves or as photons. For the purpose of atmospheric science, we will generally consider radiation as a wave rather than a photon particle. Electromagnetic radiation is a type of energy produced by electric and magnetic fields, taking a variety of names depending on the wavelength. For example, you’ve probably heard of radio waves and x-rays, whereby the primary difference is the wavelength of the waves in each. The next image shows the relationship between wavelength, frequency, and temperature. We will go into further detail later, but colder objects radiate at lower frequencies and longer wavelengths, and warmer objects radiate at higher frequency and shorter wavelengths. This relationship holds true across all scales, from atomic nuclei to planets, and across temperatures from near absolute zero to 10s of millions of Kelvins.

Wave Propagation
How fast does the Sun’s electromagnetic radiation travel to Earth and how can we characterize the waves? All electromagnetic waves travel at the speed of light (often given the variable “c0“, approximately 3×108 m·s–1). The waves have a wavelength (λ) given by the distance from one wave crest to the next. The waves also have a frequency (v), which is the number of repeated wave occurrences in a specified period of time. The unit for frequency is Hertz (cycles per second). Finally, one can also define a wavenumber for waves, which is one over the wavelength, or the number of waves in each meter, σ (cycles·m–1) = 1 / λ. Circular frequency is defined as ω (radians·s–1) = 2π·ν.
![]()
![]()
With variables for wavelength and frequency, we can very clearly define any type of wave.
Hawaii Focus Box
Electromagnetic waves are simply a type of wave. They can be described with some of the same words and variables as ocean waves. If you are a surfer, you probably check the swell forecast for wave height and wave period before you head out to the water. The best waves for surfing have a long period, which helps to separate and clearly define individual waves. Wave periods larger than 12 or 14 seconds are ideal. Depending on whether you are a beginner or advanced, you might like to have a wave face height between 2 and 30 feet, respectively.

Wave period is defined as the time it takes for a wave to complete one cycle. Wave period is simply the inverse of wave frequency.
Wave face height is related to both wave amplitude and frequency, but is much more complicated because in the case of surfing, it is measured as the wave breaks. In the case of electromagnetic energy, the waves do not break.
Characterizing Emission
Where does this electromagnetic energy come from? It surrounds us every moment of every day in many forms. In fact, any object warmer than absolute zero (0 K) emits radiant energy. In order to estimate the amount of radiant energy an object emits, a common simplification is needed: we assume an object behaves as a blackbody. A blackbody is an object that emits and absorbs the maximum amount of radiation possible given its temperature.
Planck’s Curves
Planck’s curves are used to show the amount of emitted radiation and primary wavelengths of electromagnetic energy that a black body emits given its temperature. The diagram below shows multiple Planck function curves for various temperature black bodies. The red line denotes an object that has a temperature of 3000 K, the green line is 4000 K, and the blue line is 5000 K. As the black body becomes hotter, it emits at shorter wavelengths and greater intensities.

Wien’s Law
Planck’s function tells us the amount of emitted radiation and wavelengths over which it is emitted given the temperature of the black body. We can use another law to determine the maximum wavelength emitted by a black body. Wien’s Law states that the shorter the wavelength emitted, the hotter (more kinetic energy) the object is. In Wien’s equation, sometimes the numerator is given as “a”, a constant equal to 2897.
![]()
![]()
Using Wein’s equation to find wavelength gives an answer in microns, µm. One micron is equal to 10-6 meters.
2.1 Solar Radiation Wavelength
Question: Our sun is a yellow dwarf star with a surface temperature near 5800 K. What is the maximum wavelength of the radiation it emits? Where does that radiation fall on the electromagnetic spectrum?
Answer: Wein’s Law gives us an equation that relates temperature to the maximum wavelength of radiation emitted by an object:
![]()
![]()
This radiation, 0.499 µm, is in the range of visible light, given as 0.5 × 10-6 m by the chart earlier this chapter.
Stefan-Boltzmann Law
One last very important law for radiation will be discussed here. The Stefan-Boltzmann Law relates the total radiation emitted (total emitted power per area) to the area under Planck’s curve. This can be used to show that the hotter the object, the more energy it radiates per unit area.
![]()
![]()
In the above equation the amount of radiance emitted per area is equal to the temperature of the black body raised to the 4th power. This relationship is extremely important. It shows that the amount of radiation emitted depends heavily on temperature such that small temperature fluctuations result in large changes in emittance.
The Stefan-Boltzmann constant is 5.67×10–8 W·m–2·K–4 and the symbol sigma, σ, is used.
Application to the Earth-Sun System
In the prior section, the discussion turned rather technical. We went down a rabbit hole of radiation wavelengths, total emitted power per area, and the assumption of black bodies. We did this so that we could understand basic relationships about the energy balance in the Earth-Sun system. The Sun’s average temperature is above 5,000 K while the Earth’s average temperature is in the range 210-310 K (we will discuss this further in a later chapter). This means that the Sun and Earth radiate energy very differently.
The Sun emits solar radiation, also known as ultraviolet radiation or shortwave radiation. The Earth emits infrared radiation or longwave radiation. This follows directly from the electromagnetic energy spectrum and the respective temperatures of the Sun and Earth. The Sun emits radiation at a shorter wavelength than the Earth because it has a higher temperature, and Planck’s curve for higher temperatures peaks at shorter wavelengths. It is for this reason that Earth’s radiation is referred to as longwave, and the Sun’s radiation is called shortwave.
We learned that a black body absorbs all incoming radiation and emits the maximum possible radiation given its temperature. In the Earth-Sun system, this means that the Earth absorbs all incoming radiation from the Sun, and emits the maximum amount given its temperature. In practice it is a little bit more complicated than this.
Albedo
Not all incoming solar radiation is absorbed by the Earth because the Earth is not a perfect black body. Instead of absorbing all incoming radiation, some of it is reflected. Reflection refers to radiative energy bouncing back away from an object. We can define albedo (α) as the ratio of the amount of radiation reflected from an object to the amount of radiation received by an object.
![]()
Earth has an albedo of about 0.3 or 30%. This is an average that takes into account the high albedo and high latitude regions that are snow covered as well as the clouds and the much lower albedo oceans. Note that radiation reflected from an object does not warm the object.
Surface Energy Balance
Arguably the most important aspect to consider about the Earth-Sun system is the energy balance. In steady-state, the amount of incoming energy should equal the amount of outgoing energy (Net Radiative Flux=F*=0).
Let’s start with the incoming solar radiation. The solar constant “S” is approximately equal to 1361 W·m-2. This value is a rough estimate of the amount of energy per area received by the Earth from the Sun, but it is not exact. We call it a solar “constant” but it can be slightly lower or higher at times. Radiation emitted from a spherical source, like the sun, decreases by the square of the distance from the sphere’s center. This is called the inverse square law.
The following equation is a basic budget equation. Net radiation (F*) is equal to the incoming solar radiation (K↓), the reflected solar radiation (K↑), the longwave radiation emitted by the Earth (I↑), and the downwelling longwave radiation emitted from the atmosphere (I↓) received by the Earth’s surface.
![]()
Some of the sunlight that reaches the surface of the Earth is reflected, depending on the albedo, K↑ is often written in the following way:
![]()
This is a brief introduction to a surface energy balance model. As you may imagine, it can become much more complicated depending on the factors involved. It also strongly depends on the number of layers considered in the model. We will discuss this further in a later chapter.

For now, you should understand that incoming solar radiation is called shortwave radiation and is in the ultraviolet and visible portions of the electromagnetic spectrum because of the emission temperature of the Sun. When solar radiation interacts with the Earth, it is partially absorbed by the Earth’s surface, and partially reflected, depending on the albedo of the surface. In the diagram above, you can see that some of the incoming solar radiation is reflected by clouds, some is reflected by the Earth’s surface, but most is absorbed by the Earth’s surface or the atmosphere.
You should also understand that Earth emits radiation too. However, it is at a lower intensity and a much longer wavelength, which is called the infrared portion of the electromagnetic spectrum because of the lower emission temperature of the Earth. Radiation is emitted by the Earth’s surface, and by the atmosphere. We’ll go into more detail on this later.
Earth’s average temperature remains relatively constant as there is a balance of outgoing radiation and incoming radiation.
Radiation Interaction with the Atmosphere
The diagram below shows the spectral intensity of downgoing solar radiation (UV and visible in red) and upgoing thermal radiation (IR in blue). The panels below the spectral intensity graph show the total percentage of radiation absorbed and scattered by the atmosphere as a function of wavelength, and divided up by the primary greenhouse gases in the atmosphere. Greenhouse gases are gases in the Earth’s atmosphere that can absorb and emit radiation, primarily infrared radiation.
The greenhouse gas that interacts with radiation across the largest number of wavelengths is water vapor (H2O), which interacts strongly with the atmosphere, especially in the longer wavelength portion of the spectrum. Other gases, such as Carbon Dioxide (CO2), Oxygen (O2), Ozone (O3), Methane (CH4), and Nitrous Oxide (NO) also interact with radiation.

In the panel of the figure above showing the total percentage of radiation that is absorbed by the Earth’s atmosphere, you’ll notice white gaps. These are called Atmospheric Windows where the wavelength of radiation is able to pass through the atmosphere without interaction with greenhouse gases. Particularly notable is the visible portion of the electromagnetic energy spectrum that can pass through the atmosphere unimpeded. Also notable is the large amount of interference in the infrared portion of the spectrum. Earth’s atmosphere is practically transparent for shortwave radiation, and it strongly absorbs infrared radiation. This will be important for climate factors discussed in a later chapter.
The interaction of atmospheric gases in Earth’s atmosphere is an important part of its energy balance. The greenhouse effect is the result of greenhouse gases absorbing and emitting outgoing infrared radiation emitted from Earth’s surface. Because Earth’s outgoing longwave radiation is partially absorbed by the atmosphere, this has a warming effect on Earth’s surface making it warmer than it would be otherwise. While the greenhouse effect has a bad reputation, this process has in fact allowed Earth to be habitable.
Radiation Changes with Time
The amount of radiation the Earth receives from the Sun varies over many time scales, from thousands of years, to one year, to daily time periods. These will be discussed in the following sections.
Changes in solar radiation on both daily and annual time scales can be explained by Earth’s orbital path around the Sun. These aspects will be discussed more thoroughly in a later chapter, but for now, let’s have a brief introduction. There are three primary factors to consider: eccentricity, obliquity, and precession. Eccentricity is the circularity of a planetary orbit. For example, a circle has zero eccentricity. Obliquity is the degree of tilt in the axis of rotation. Finally, precession is the wobble in the rotational axis of a planet that slowly traces out a cone. The three orbital parameters are shown in the image below.
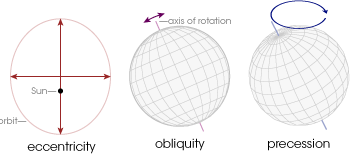
Currently the Earth has a 0.0167 orbital eccentricity, 23.44 degree tilt from vertical, and precesses on very long time scales. In fact, all of these factors change slightly over very long time scales but for now, let’s consider them to be constant.
Seasonal Changes
Seasons occur due to changes in solar radiation that come from the position of Earth with respect to the Sun. The diagram below shows the position of the Earth with respect to the sun during each of the four seasons.
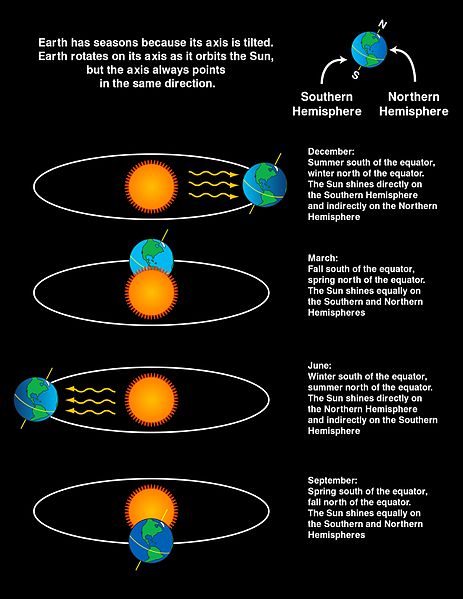
During summertime in each hemisphere, the hemisphere is facing toward the sun. For example, in June in the Northern Hemisphere summer, the sun shines more directly on the Northern Hemisphere than the Southern Hemisphere. While it seems like a small change, the sun angle and the amount of solar radiation absorbed (per area) varies significantly throughout the year. This is because in addition to changing the angle of the Sun, the position of the Earth also changes the length of day throughout the year. Seasons are due to the tilt of the Earth. If the Earth’s rotation was not tilted, it would not have seasonal changes.
The diagram below shows the summer season in the Southern Hemisphere where there is a higher density of incident rays due to the higher Sun angle. The Northern Hemisphere is experiencing wintertime. When the Sun’s rays are at an angle as they are in the Northern Hemisphere, the same amount of energy is spread over a larger area than they would be if the Sun’s rays were perpendicular to the surface. Again, the angle of the Sun’s rays and the length of day change because of the Earth’s tilt.

Daily Changes
Daily changes are also called “diurnal.” The Earth absorbs radiation from the Sun during the daytime. This is only true for one location, but accounts for the increase in temperature throughout the day from a point perspective. What we likely have not experienced directly is that the Earth emits infrared radiation all day and night. The lack of incoming solar radiation and the emission of infrared radiation is what accounts for the decrease in temperature at night. The combination of nonstop outgoing longwave radiational cooling from Earth’s radiative emissions and daytime solar shortwave radiational heating results in a diurnal cycle of net radiation and temperature, as seen below.

In this chapter we focused on the radiation: how we can define and describe it by wavelength and intensity; the temperatures it corresponds to as well as how it changes over time scales. As a reminder, these were our learning goals:
- Define black body radiation and Planck’s Law
- Apply Wien’s law to compute the maximum emission wavelength
- Use Stefan-Boltzmann’s law to compute radiative emittance
- Describe Earth’s surface radiation budget, including shortwave and longwave components
- Define and differentiate obliquity, eccentricity, and precession
- Describe the cause of seasons on Earth
- Describe the diurnal cycle of radiative fluxes
In the following chapter, we’ll begin to see how this radiation does work, and what that means for the environment.
Chapter 2: Questions to Consider
- Are the following statements about radiation true or false?
- Describe the relationship between wavelength, energy emission, and the temperature of an object.
- If the temperature of the Earth is 257 K, what is the total radiative flux emitted? What is the peak emission wavelength?
- How would the seasons change if the Earth’s tilt were greater?
Selected Practice Question Answers: