Fractions
Dividing Fractions: Invert and Multiply
The missing factor method is a particularly nice way to understand fraction division. It builds on what we know about multiplication and division, reinforcing that these operations have the same relationship whether the numbers are whole number, fractions, or anything else. It makes sense. But we’ve seen that it doesn’t always work out nicely. For example,
![]()
can be rewritten as
![]()
You want to ask:
- For the numerator:
 . We can fill in the blank with a 3.
. We can fill in the blank with a 3. - For the denominator:
 . We can fill in the blank with
. We can fill in the blank with 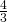 . (Why does that work?)
. (Why does that work?)
So we have:
![]()
You learned about fractions like
![]()
back in the “What is a Fraction?” chapter. This means that each ![]() of a kid gets 3 pies. So how much does an individual kid (one whole kid) get? You could draw a picture to help you figure it out. But we can also use the key fraction rule to help us out.
of a kid gets 3 pies. So how much does an individual kid (one whole kid) get? You could draw a picture to help you figure it out. But we can also use the key fraction rule to help us out.
![]()
This process is going to be key to understanding why the “invert and multiply” rule for fraction division actually makes sense.
Simplify an Ugly Fraction
Example
![]() pies are shared equally by
pies are shared equally by ![]() children. How much pie does each child get?
children. How much pie does each child get?
Technically, we could just write down the answer as
![]()
and be done! The answer is equivalent to this fraction, so why not?
Is there a way to make this look friendlier? Well, if we change those mixed numbers to “improper” fractions, it helps a little:
![]()
That’s a bit better, but it’s still not clear how much pie each kid gets. Let’s use the key fraction rule to make the fraction even friendlier. Let’s multiply the numerator and denominator each by 3. (Why three?) Remember, this means we’re multiplying the fraction by ![]() , which is just a special form of 1, so we don’t change its value.
, which is just a special form of 1, so we don’t change its value.
![]()
Now multiply numerator and denominator each by 4. (Why four?)
![]()
We now see that the answer is ![]() . That means that sharing
. That means that sharing ![]() pies among
pies among ![]() children is the same as sharing 92 pies among 63 children. (In both situations, the individual child get exactly the same amount of pie.)
children is the same as sharing 92 pies among 63 children. (In both situations, the individual child get exactly the same amount of pie.)
Example
Let’s forget the context now and just focus on the calculations so that we can see what is going on more clearly. Try this one:
![]()
Multiplying the numerator and denominator each by 5 (why did we choose 5?) gives
![]()
Now multiply the numerator and denominator each by 3 (why did we choose 3?):
![]()
On Your Own
- Each of the following is a perfectly nice fraction, but it could be written in a simpler form. So do that! Write each of them in a simpler form following the examples above.
![]()
Think / Pair / Share
- Jessica calculated the second exercise above this way:
![]()
Is her solution correct, or is she misunderstanding something? Carefully explain what is going on with her solution, and what you would do as Jessica’s teacher.
- Isaac calculated the last exercise above this way:
![]()
Is his solution correct, or is he misunderstanding something? Carefully explain what is going on with his solution, and what you would do as Isaac’s teacher.
Perhaps without realizing it, you have just found another method to divide fractions.
Example: 3/5 ÷ 4/7
Consider ![]() . We know that a fraction is the answer to a division problem, meaning
. We know that a fraction is the answer to a division problem, meaning
![]()
And now we know how to simplify ugly fractions like this one! Multiply the numerator and denominator each by 5:
![]()
Now multiply them each by 7:
![]()
Done! So
![]()
Example: 5/9 ÷ 8/11
Let’s do another! Consider ![]() :
:
![]()
Let’s multiply numerator and denominator each by 9 and by 11 at the same time. (Why not?)
![]()
(Do you see what happened here?)
So we have
![]()
On Your Own
Compute each of the following, using the simplification technique in the examples above.
![]()
Invert and multiply
Consider the problem ![]() . Janine wrote:
. Janine wrote:
![]()
She stopped before completing her final step and exclaimed: “Dividing one fraction by another is the same as multiplying the first fraction with the second fraction upside down!”
Think / Pair / Share
First check each step of Janine’s work here and make sure that she is correct in what she did up to this point. Then answer these questions:
- Do you understand what Janine is saying? Explain it very clearly.
- Work out
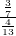 using the simplification method. Is the answer the same as
using the simplification method. Is the answer the same as  ?
? - Work out
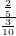 using the simplification method. Is the answer the same as
using the simplification method. Is the answer the same as 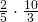 ?
? - Work out
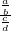 using the simplification method. Is the answer the same as
using the simplification method. Is the answer the same as 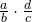 ?
? - Is Janine right? Is dividing two fractions always the same as multiplying the two fractions with the second one turned upside down? What do you think? (Do not just think about examples. This is a question if something is always true.)
Summary
We now have several methods for solving problems that require dividing fractions:
Dividing fractions:
- Draw a picture using the rectangle method, and use that to solve the division problem.
- Find a common denominator and divide the numerators.
- Rewrite the division as a missing factor multiplication problem, and solve that problem.
- Simplify an ugly fraction.
- Invert the second fraction (the dividend) and then multiply.
Think / Pair / Share
Discuss your opinions about our four methods for solving fraction division problems with a partner:
- Which method for division of fractions is the easiest to understand why it works ?
- Which method for division of fractions is the easiest to use in computations?
- What are the benefits and drawbacks of each method? (Think both as a future teacher and as someone solving math problems here.)
