Patterns and Algebraic Thinking
Structural and Procedural Algebra
When most people think about algebra from school, they think about “solving for ![]() .” They imagine lots of equations with varying levels of complexity, but the goal is always the same: find the unknown quantity. This is a procedural view of algebra.
.” They imagine lots of equations with varying levels of complexity, but the goal is always the same: find the unknown quantity. This is a procedural view of algebra.
Even elementary students can be exposed to ideas in procedural algebra. This happens any time they think about unknown quantities and try to solve for them. For example, when first grade students learn to add and subtract numbers “within 10,’” they should frequently tackle problems like these:
 .
.- Find several pairs of numbers that add up to 10.
Although procedural algebra is important, it’s not the most important skill, and it’s certainly not the whole story.
You also need to foster thinking about structural algebra in your students: using symbols to express meaning in a situation. If there is an x on your page, you should be able to answer, “what does the x mean? What does it represent?”
Most of what you’ve done so far in this chapter is structural algebra. You’ve used letters and symbols not to represent a single unknown quantity, but a varying quantity. For example, in Section 4 you used letters to represent the “figure number’” or “case number” in a growing pattern. The letters could take on different values, and the expressions gave you information: how many tiles or toothpicks or stars you needed to build that particular figure in that particular pattern.
Think / Pair / Share
- Consider the expression
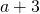 . Give a real world situation that could be represented by this expression. Share your answer with your partner. Together, can you come up with even more ideas?
. Give a real world situation that could be represented by this expression. Share your answer with your partner. Together, can you come up with even more ideas? - Suppose the expression
 represents the number of tiles used at any stage of a growing pattern.
represents the number of tiles used at any stage of a growing pattern.
-
- Evaluate the expression at
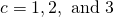 . What do the values tell you about the pattern?
. What do the values tell you about the pattern? - Can you describe in words how the pattern is growing?
- Can you design a pattern with tiles that grows according to this rule?
- Where do you see the “3” in your pattern? Where do you see the “2”’? Where do you see the “
 ”?
”?
- Evaluate the expression at
Problem 21
Krystal was looking at this pattern, which may be familiar to you from the Problem Bank:

She wrote down the equation
![]()
In Krystal’s equation, what does ![]() represent? What does
represent? What does ![]() represent? How do you know?
represent? How do you know?
Problem 22
Candice was thinking about this problem:
Today is Jennifer’s birthday, and she’s twice as old as her brother. When will she be twice as old as him again?
She wrote down the equation ![]() . In Candice’s equation, what does
. In Candice’s equation, what does ![]() represent? What does
represent? What does ![]() represent? How do you know?
represent? How do you know?
Problem 23
Sarah and David collect old coins. Suppose the variable ![]() stands for the number of coins Sarah has in her collection, and
stands for the number of coins Sarah has in her collection, and ![]() stands for the number of coins David has in his collection. What would each of these equations say about their coin collections?
stands for the number of coins David has in his collection. What would each of these equations say about their coin collections?
![]()
Problem 24
The pictures below show balance scales containing bags and blocks. The bags are marked with a “?”’ because they contain some unknown number of blocks. In each picture:
- Each bag contains the same number of blocks.
- The scale is balanced.
For each picture, determine how many blocks are in each bag. Justify your answers.

(a)

(b)

(c)
Problem 25
When he was working on Problem 24, Kyle wrote down these three equations.
(i) ![]() .
.
(ii) ![]() .
.
(iii) ![]() .
.
Match each equation to a picture, and justify your choices. Then solve the equations, and say (in a sentence) what the solution represents.
Problem 26
Draw a balance puzzle that represents the equation
![]()
Now solve the balance puzzle. Where is the “![]() ” in your puzzle? What does it represent?
” in your puzzle? What does it represent?
Problem 27
Draw a balance puzzle that represents the equation
![]()
Now solve the equation. Explain what happens.
Problem 28
Which equation below is most like the one in Problem 27 above? Justify your choice.
![]()
![]()
Problem 29
Draw a balance puzzle that represents the equation
![]()
Now solve the equation. Explain what happens.
Problem 30
Which equation below is most like the one in Problem 29 above? Justify your choice.
![]()
![]()
Problem 31
Create a balance puzzle where the solution is not a whole number of blocks. Can you solve it? Explain your answer.
Problem 32
There are three piles of rocks: pile A, pile B, and pile C. Pile B has two more rocks than pile A. Pile C has four times as many rocks as pile A. The total number of rocks in all three piles is 14.
- Use x to represent the number of rocks in pile A, and write equations that describe the rules above. Then find the number of rocks in each pile.
- Use x to represent the number of rocks in pile B, and write equations that describe the rules above. Then find the number of rocks in each pile.
- Use x to represent the number of rocks in pile C, and write equations that describe the rules above. Then find the number of rocks in each pile.
Think / Pair / Share
Look back at Problems 21–32. Which of them felt like structural algebraic thinking? Which felt like procedural algebraic thinking? Did any of the problems feel like they involved both kinds of thinking?
Variables and Equations
You have seen that in algebra, letters and symbols can have different meanings depending on the context.
- A symbol could stand for some unknown quantity.
- A symbol could stand for some quantity that varies. (Hence the term “variable” to describe these symbols.)
In much the same way, equations can represent different things.
- They can represent a problem to be solved. This is the traditional procedural algebra type of question.
- They can represent a relationship between two or more quantities. For example,
 represents the relationship between the area of a square and its side length.
represents the relationship between the area of a square and its side length. - They can represent identities: mathematical truths. For example,
![Rendered by QuickLaTeX.com \[x^2 - 1 = (x+1)(x-1)\]](http://pressbooks-dev.oer.hawaii.edu/math111/wp-content/ql-cache/quicklatex.com-18131bd0a709e30f3dc7b0fc76d802c8_l3.png)
is always true, for every value of
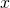 . There is nothing to solve for, and no relationship between varying quantities. (If you do try to “solve for
. There is nothing to solve for, and no relationship between varying quantities. (If you do try to “solve for 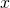 ,” you will get the equation
,” you will get the equation 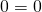 , much like you saw in Problem 29. Not very satisfying!)
, much like you saw in Problem 29. Not very satisfying!)
Think / Pair / Share
Give an example of each type of equation. Be sure to say what the symbols in the equations represent.
Problem 33
Answer the following questions about the equation
![]()
- Evaluate both sides of the above equation for
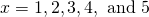 . What happens?
. What happens? - Use the distributive property of multiplication over addition to expand the right side of the equation and simplify it.
- Use the equation to compute
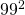 quickly, without using a calculator. Explain how you did it.
quickly, without using a calculator. Explain how you did it.
