Place Value
Problem Bank
Problem 28
- If you were counting in base four, what number would you say just before you said
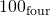 ?
? - What number is one more than
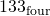 ?
? - What is the greatest three-digit number that can be written in base four? What numbers come just before and just after that number?
Problem 29
Explain what is wrong with writing ![]() or
or ![]() .
.
Problem 30
- Write out the base three numbers from
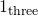 to
to 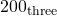 .
. - Write out the base five numbers from
 to
to 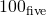 .
. - Write the four base six numbers that come after
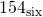 .
.
Problem 31
Convert each base ten number to a base four number. Explain how you did it.
![]()
Challenges:
![]()
Problem 32
In order to use base sixteen, we need sixteen digits — they will represent the numbers zero through fifteen. We can use our usual digits 0–9, but we need new symbols to represent the digits ten, eleven, twelve, thirteen, fourteen, and fifteen. Here’s one standard convention:
| base ten | base sixteen |
|---|---|
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 |
- Convert these numbers from base sixteen to base ten, and show your work:
![Rendered by QuickLaTeX.com \[ 6\textrm{D}_{\text{sixteen}} \qquad \quad \textrm{AE}_{\text{sixteen}} \qquad\quad 9\textrm{C}_{\text{sixteen}} \qquad\quad 2\textrm{B}_{\text{sixteen}} \]](http://pressbooks-dev.oer.hawaii.edu/math111/wp-content/ql-cache/quicklatex.com-d30f57a17f219be7660bb03a91941dc8_l3.png)
- Convert these numbers from base ten to base sixteen, and show your work:
![Rendered by QuickLaTeX.com \[97 \qquad \quad 144 \qquad\quad 203 \qquad\quad 890 \]](http://pressbooks-dev.oer.hawaii.edu/math111/wp-content/ql-cache/quicklatex.com-89d12cbc8359e6d2dd96d1da1b68d0fd_l3.png)
Problem 33
How many different symbols would you need for a base twenty-five system? Justify your answer.
Problem 34
All of the following numbers are multiples of three.
![]()
- Identify the powers of 3 in the list. Justify your answer.
- Write each of the numbers above in base three.
- In base three: how can you recognize a multiple of 3? Explain your answer.
- In base three: how can you recognize a power of 3? Explain your answer.
Problem 35
All of the following numbers are multiples of five.
![]()
- Identify the powers of 5 in the list. Justify your answer.
- Write each of the numbers above in base five.
- In base five: how can you recognize a multiple of 5? Explain your answer.
- In base five: how can you recognize a power of 5? Explain your answer.
Problem 36
Convert each number to the given base.
 into base eight.
into base eight.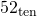 into base two.
into base two.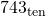 into base five.
into base five.
Problem 37
What bases makes theses equations true? Justify your answers.
Problem 38
What bases makes theses equations true? Justify your answers.
Problem 39
- Find a base ten number that is twice the product of its two digits. Is there more than one answer? Justify what you say.
- Can you solve this problem in any base other than ten?
Problem 40
- I have a four-digit number written in base ten. When I multiply my number by four, the digits get reversed. Find the number.
- Can you solve this problem in any base other than ten?
Problem 41
Convert each base four number to a base ten number. Explain how you did it.
![]()
Challenges:
![]()
Problem 42
Consider this base ten number (I got this by writing the numbers from 1 to 60 in order next to one another):
![]()
- What is the largest number that can be produced by erasing one hundred digits of the number? (When you erase a digit it goes away. For example, if you start with the number 12345 and erase the middle digit, you produce the number 1245.) How do you know you got the largest possible number?
- What is the smallest number that can be produced by erasing one hundred digits of the number? How do you know you got the smallest possible number?
Problem 43
Can you find two different numbers (not necessarily single digits!) ![]() and
and ![]() so that
so that ![]() ? Can you find more than one solution? Justify your answers.
? Can you find more than one solution? Justify your answers.
